MPC Controller for a Rocket Prototype

Advanced control systems for a rocket prototype using Model Predictive Control.

This project explores the development and application of various Model Predictive Control (MPC) strategies for a rocket prototype using thrust vector control. The project was undertaken as part of the ME-425 course on Model Predictive Control at EPFL.

You can find the PDF version of the report for this project here.

The study involved system analysis, and the design of controllers tailored to both the linearized system, as well as the full nonlinear dynamics using a non linear optimizer. The controllers were evaluated for performance, robustness, and feasibility under varying conditions, including time delays.

This is a group project, see the PDF report for more details about the group members.

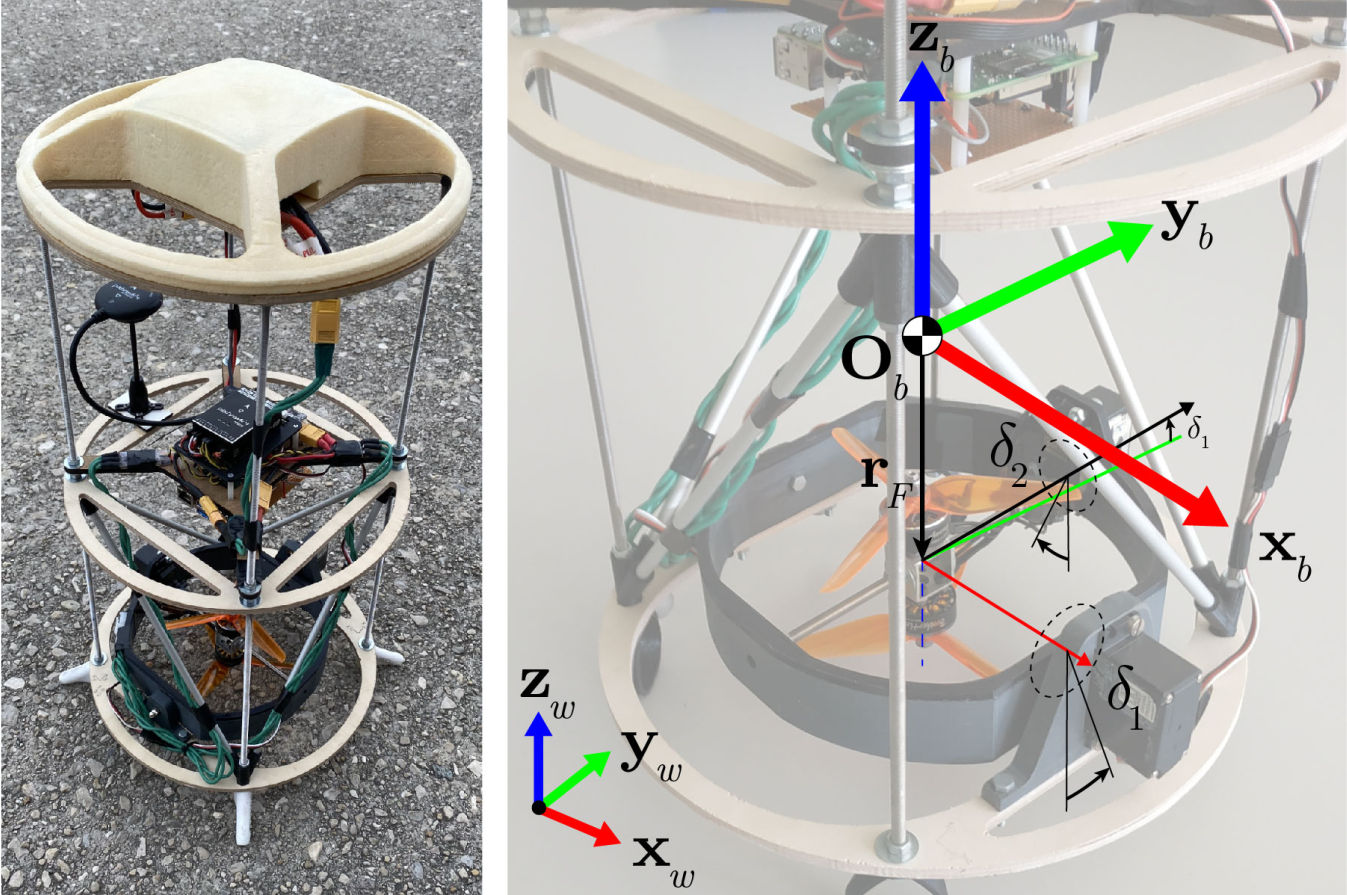
Rocket prototype used for the study.

Linearization and Subsystem Separation

The rocket’s nonlinear dynamics, comprising 12 states and 4 inputs, were linearized around a steady-state trim point. Subsystems were separated into four decoupled controllers:

  • Subsystem X: Controlling the x-axis movement.
  • Subsystem Y: Controlling the y-axis movement.
  • Subsystem Z: Managing vertical motion.
  • Subsystem Roll: Regulating roll dynamics.

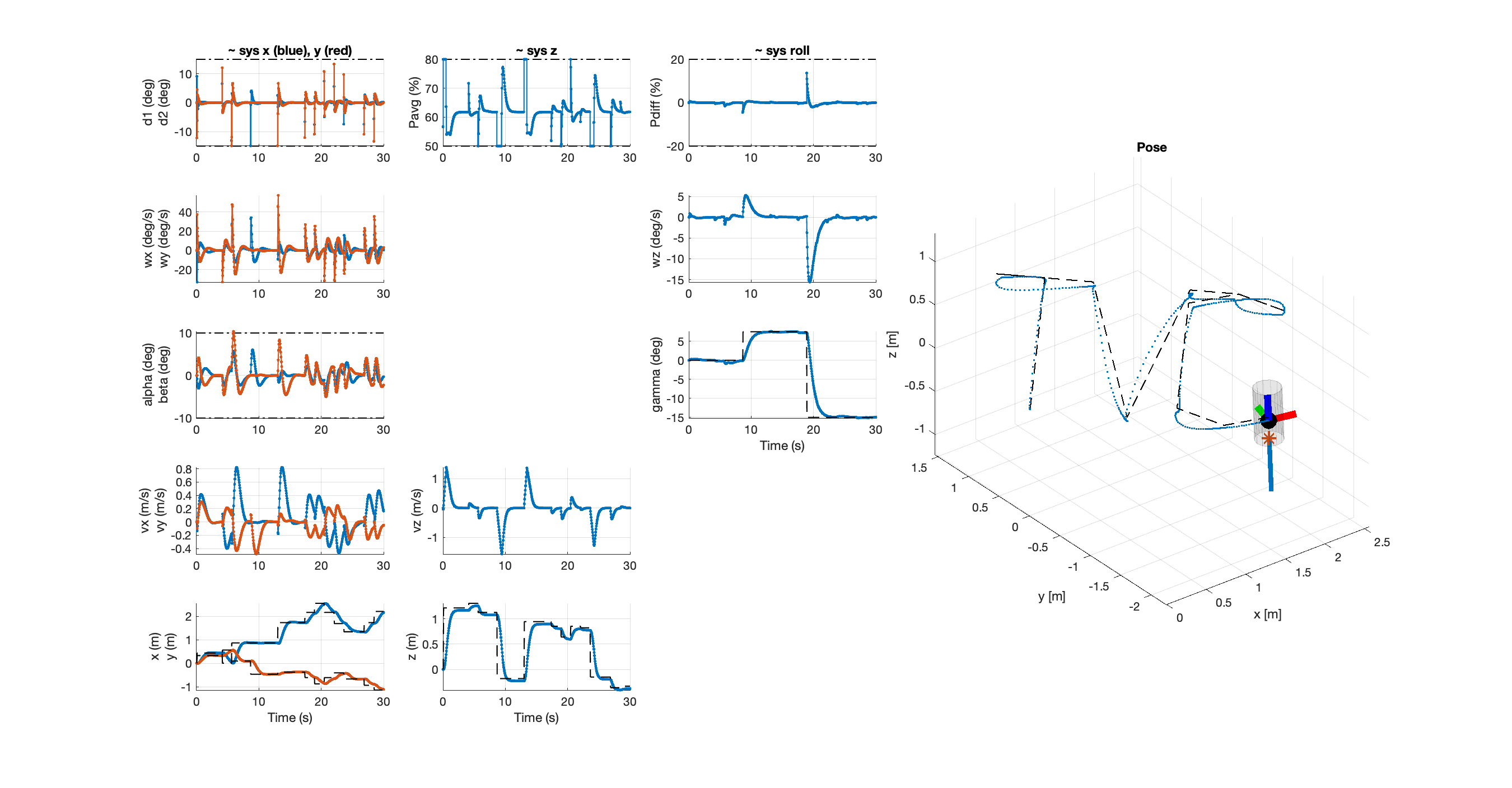
MPC Controllers

Four independent MPC regulators were designed for each subsystem to stabilize the system and track reference trajectories. Techniques included:

  • Recursive feasibility through invariant sets.
  • Constraint softening to handle mismatches.

Simulations demonstrated the controllers’ success in tracking reference points and maintaining stability.

Linear MPC under limiting roll constraints.

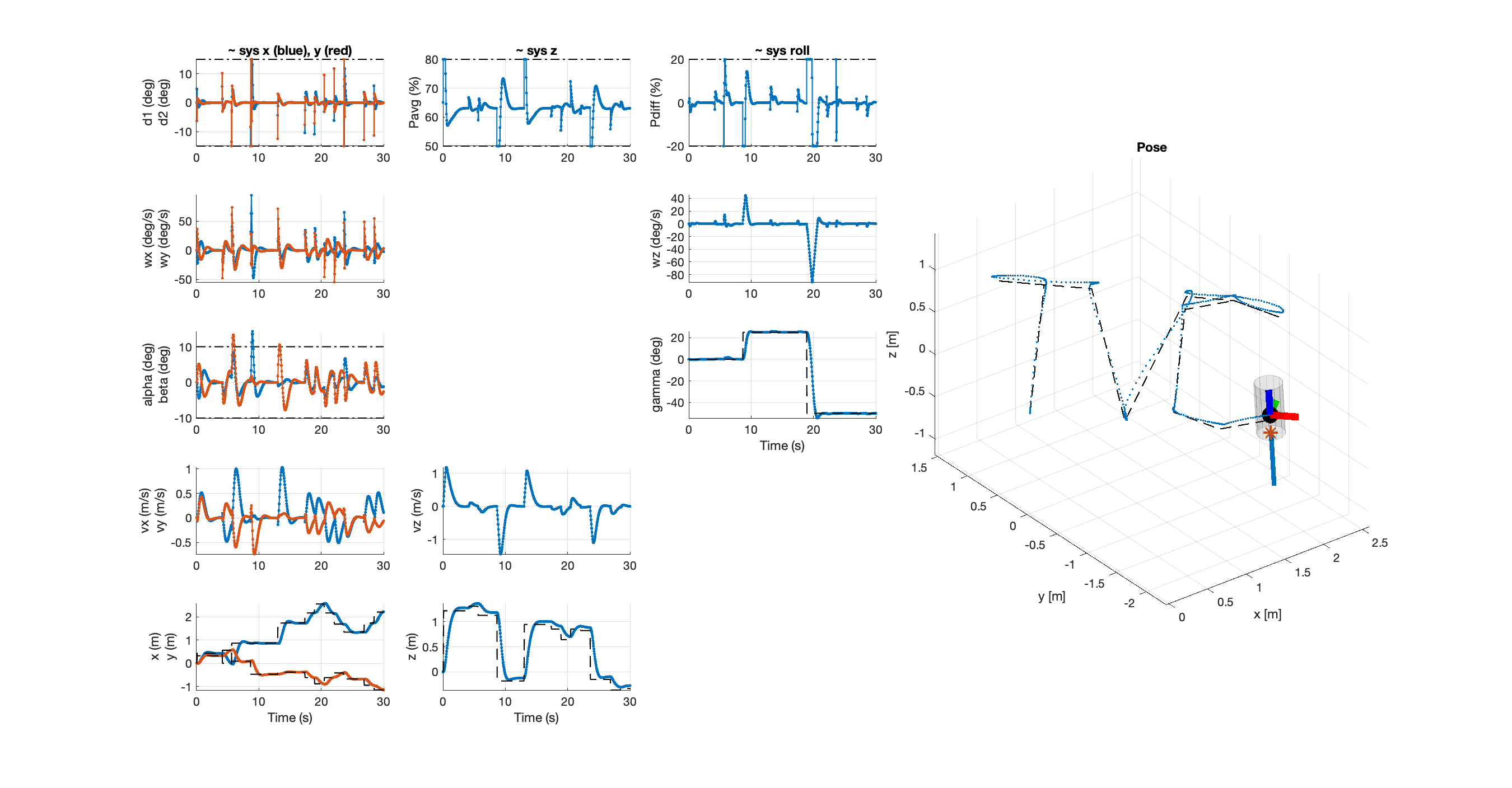
Nonlinear MPC

To manage the rocket’s full nonlinear dynamics, a Nonlinear Model Predictive Controller (NMPC) was implemented using the CASADI framework. This controller enabled to control the full state-space system without subsystem decomposition.

Comparative analyses revealed the NMPC’s superior handling of nonlinear dynamics, particularly under high roll angle constraints.

Nonlinear MPC performance.

Conclusion

This project highlights the power and versatility of MPC strategies in managing complex, nonlinear dynamic systems. The insights gained from this study can inform the design of advanced control systems for aerospace applications and beyond.